Accueil > Publications > Quelques triplets Pythagoriciens primitifs, triangles rectangles et (...)
Triplets d’entiers pythagoriciens primitifs - Triangles Rectangles - Nombres Complexes - Non Semblables
 Quelques triplets Pythagoriciens primitifs, triangles rectangles et nombres complexes non semblables.
Quelques triplets Pythagoriciens primitifs, triangles rectangles et nombres complexes non semblables.
Données
mardi 19 septembre 2006, par
Voici pour des exercices :
- des mesures de côtés de triangles rectangles non semblables c’est à dire pour lesquels il n’existe pas de similitude entre triangle triangle de la liste et dont les mesures des côtés sont des nombres entiers.
- cette liste peut aussi être utilisée pour générer des exercices sur des nombres complexes dont le module sont des entiers ou des décimaux.
- cette liste est un sous-ensemble des triplets Pythagoriciens.
Le triangle 3 4 5 n’est pas le seul triangle rectangle ayant des mesures entières, c’est simplement le plus facile à retenir mais aussi le premier d’une série de triangle. On peut obtenir d’autres triangles rectangles en multipliant les mesures 3 ; 4 et 5 des côtés par un même nombre, par exemple 1,5 : 4,5 ; 6 ; 7,5 ou par 2 : 6, 8, 10 ...
Attention, il ne faut pas en conclure que tout triangle rectangle ayant des mesures entières est obtenu à partir du triangle 3 4 5 !
Voici pour des exercices, des triangles rectangles non homothétiques, dont les mesures des côtés ![]() sont des nombres entiers :
sont des nombres entiers :
Ils vérifient la relation ![]()
Exemples :
- Théorème de Pythagore
- Calculer la mesure de l’hypoténuse d’un triangle rectangle dont les deux autres côtés ont pour mesures 83,7 et 11,6 : Les calculs conduisent à 84,5. Les trois mesures sont obtenues en divisant chaque nombre du triplet (845, 837, 116) par 10.
- En changeant le facteur, on peut obtenir, un grand nombre d’exercices dont on maîtrise les résultats au niveau de la précision.
- Réciproque :
- Montrer que le triangle dont les côtés mesurent : 5,05 ; 3,77 et 3,36 est bien un triangle rectangle.
- Attention ! Ce n’est pas la réciproque qui permet de conclure en cas d’inégalité. C’est le théorème de Pythagore ou plus exactement sa contraposition. La réciproque permet de conclure uniquement en cas d’égalité.
- Nombres complexes :
- Calculez le module de
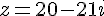 ,
, 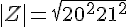 on obtient
on obtient 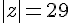
- Calculez le module de
La liste ci-dessous a été obtenue à l’aide d’un programme informatique en Pascal. L’algorithme effectue une recherche pour obtenir
– un classement par ordre croissant de la plus grande valeur,
– en conservant uniquement les triplets constitués de nombres premiers entre eux.
| a | b | c | - | a | b | c | - | a | b | c | - | a | b | c |
| 5 | 4 | 3 | 425 | 304 | 297 | 845 | 837 | 116 | 1229 | 1221 | 140 | |||
| 13 | 12 | 5 | 445 | 437 | 84 | 853 | 828 | 205 | 1237 | 1075 | 612 | |||
| 17 | 15 | 8 | 449 | 351 | 280 | 857 | 825 | 232 | 1241 | 1160 | 441 | |||
| 25 | 24 | 7 | 485 | 476 | 93 | 865 | 816 | 287 | 1249 | 960 | 799 | |||
| 29 | 21 | 20 | 493 | 468 | 155 | 881 | 800 | 369 | 1261 | 1140 | 539 | |||
| 37 | 35 | 12 | 493 | 475 | 132 | 901 | 780 | 451 | 1261 | 1189 | 420 | |||
| 53 | 45 | 28 | 505 | 377 | 336 | 905 | 663 | 616 | 1285 | 924 | 893 | |||
| 65 | 56 | 33 | 509 | 459 | 220 | 905 | 777 | 464 | 1285 | 1116 | 637 | |||
| 65 | 63 | 16 | 521 | 440 | 279 | 937 | 912 | 215 | 1289 | 1161 | 560 | |||
| 73 | 55 | 48 | 533 | 525 | 92 | 941 | 741 | 580 | 1297 | 1295 | 72 | |||
| 85 | 84 | 13 | 545 | 513 | 184 | 949 | 851 | 420 | 1313 | 1088 | 735 | |||
| 89 | 80 | 39 | 557 | 532 | 165 | 949 | 900 | 301 | 1313 | 1288 | 255 | |||
| 97 | 72 | 65 | 565 | 403 | 396 | 953 | 728 | 615 | 1345 | 1247 | 504 | |||
| 109 | 91 | 60 | 565 | 493 | 276 | 965 | 957 | 124 | 1361 | 1240 | 561 | |||
| 125 | 117 | 44 | 569 | 520 | 231 | 977 | 945 | 248 | 1369 | 1081 | 840 | |||
| 145 | 144 | 17 | 577 | 575 | 48 | 985 | 697 | 696 | 1373 | 1365 | 148 | |||
| 149 | 140 | 51 | 593 | 465 | 368 | 985 | 864 | 473 | 1381 | 1020 | 931 | |||
| 157 | 132 | 85 | 601 | 551 | 240 | 997 | 925 | 372 | 1385 | 1216 | 663 | |||
| 169 | 120 | 119 | 617 | 608 | 105 | 1009 | 840 | 559 | 1385 | 1353 | 296 | |||
| 173 | 165 | 52 | 625 | 527 | 336 | 1013 | 1012 | 45 | 1405 | 1333 | 444 | |||
| 185 | 176 | 57 | 629 | 460 | 429 | 1021 | 779 | 660 | 1409 | 1400 | 159 | |||
| 193 | 168 | 95 | 629 | 621 | 100 | 1025 | 897 | 496 | 1417 | 1175 | 792 | |||
| 205 | 187 | 84 | 641 | 609 | 200 | 1025 | 1023 | 64 | 1417 | 1392 | 265 | |||
| 221 | 171 | 140 | 685 | 667 | 156 | 1033 | 1015 | 192 | 1429 | 1380 | 371 | |||
| 221 | 220 | 21 | 685 | 684 | 37 | 1037 | 812 | 645 | 1433 | 1305 | 592 | |||
| 229 | 221 | 60 | 689 | 561 | 400 | 1037 | 988 | 315 | 1445 | 1364 | 477 | |||
| 233 | 208 | 105 | 689 | 680 | 111 | 1049 | 999 | 320 | 1453 | 1435 | 228 | |||
| 241 | 209 | 120 | 697 | 528 | 455 | 1061 | 861 | 620 | 1465 | 1127 | 936 | |||
| 257 | 255 | 32 | 697 | 672 | 185 | 1073 | 952 | 495 | 1465 | 1344 | 583 | |||
| 265 | 247 | 96 | 701 | 651 | 260 | 1073 | 975 | 448 | 1469 | 1269 | 740 | |||
| 269 | 260 | 69 | 709 | 660 | 259 | 1097 | 928 | 585 | 1469 | 1419 | 380 | |||
| 289 | 240 | 161 | 725 | 627 | 364 | 1105 | 817 | 744 | 1481 | 1120 | 969 | |||
| 293 | 285 | 68 | 725 | 644 | 333 | 1105 | 1073 | 264 | 1489 | 1320 | 689 | |||
| 305 | 273 | 136 | 733 | 725 | 108 | 1109 | 1100 | 141 | 1493 | 1395 | 532 | |||
| 313 | 312 | 25 | 745 | 624 | 407 | 1117 | 1092 | 235 | 1513 | 1225 | 888 | |||
| 317 | 308 | 75 | 745 | 713 | 216 | 1129 | 1080 | 329 | 1517 | 1292 | 795 | |||
| 325 | 253 | 204 | 757 | 595 | 468 | 1145 | 903 | 704 | 1517 | 1508 | 165 | |||
| 349 | 299 | 180 | 769 | 600 | 481 | 1145 | 1064 | 423 | 1525 | 1517 | 156 | |||
| 353 | 272 | 225 | 773 | 748 | 195 | 1153 | 1025 | 528 | 1537 | 1488 | 385 | |||
| 365 | 357 | 76 | 785 | 736 | 273 | 1157 | 868 | 765 | 1537 | 1505 | 312 | |||
| 373 | 275 | 252 | 785 | 783 | 56 | 1181 | 1131 | 340 | 1565 | 1173 | 1036 | |||
| 377 | 345 | 152 | 793 | 665 | 432 | 1189 | 989 | 660 | 1565 | 1323 | 836 | |||
| 377 | 352 | 135 | 793 | 775 | 168 | 1189 | 1020 | 611 | 1585 | 1224 | 1007 | |||
| 389 | 340 | 189 | 797 | 572 | 555 | 1193 | 855 | 832 | 1585 | 1457 | 624 | |||
| 397 | 325 | 228 | 809 | 759 | 280 | 1201 | 1200 | 49 | 1597 | 1428 | 715 | |||
| 401 | 399 | 40 | 821 | 700 | 429 | 1205 | 1107 | 476 | 1601 | 1599 | 80 | |||
| 409 | 391 | 120 | 841 | 840 | 41 | 1213 | 1188 | 245 | 1609 | 1591 | 240 | |||
| 421 | 420 | 29 | 845 | 836 | 123 | 1217 | 992 | 705 | 1613 | 1275 | 988 |